Skip to main content

Graph

A Graph is a non-linear data structure consisting of vertices and edges. The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph is composed of a set of vertices( V ) and a set of edges( E ). The graph is denoted by G(V, E)

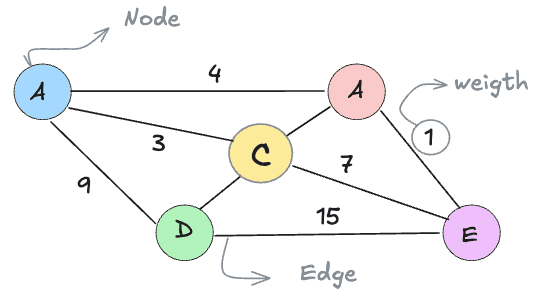
Graph

Components of a Graph​

Vertices: These are the fundamental units or nodes in a graph. Each vertex can represent an entity such as a city, person, or point of interest.

Edges: These are the connections between the vertices. An edge may be directed (indicating a one-way relationship) or undirected (indicating a mutual relationship). For example, a one-way street between two locations would be represented by a directed edge, while a mutual friendship would be represented by an undirected edge.

Weights: Graphs can be either weighted or unweighted. Weights on the edges represent costs, distances, or any quantifiable metric that impacts the connection between two vertices. For instance, in a road map, weights might represent the distance or time taken to travel between locations.

Types of Graphs​

Undirected Graph: In an undirected graph, edges have no direction. This means that if there is an edge between vertex A and vertex B, you can traverse from A to B and from B to A equally

Directed Graph (Digraph): In a directed graph, each edge has a direction. If there is a directed edge from vertex A to vertex B, you can only traverse from A to B and not necessarily from B to A unless there is a corresponding edge in that direction

Weighted Graph: Each edge in a weighted graph has a numeric value associated with it. These weights can represent quantities like cost, length, or capacity, depending on the context of the problem being solved

Unweighted Graph: In an unweighted graph, the edges do not have weights. This simplifies the model where the only information of interest is whether a pair of vertices is connected or not

Cyclic Graph: A cyclic graph contains at least one graph cycle, i.e., a path of edges and vertices wherein a vertex is reachable from itself

Acyclic Graph: An acyclic graph is a graph without cycles. For directed graphs, this is often referred to as a Directed Acyclic Graph (DAG). DAGs are especially important in scenarios like task scheduling and dependencies where cycles could cause deadlocks or inconsistencies

Adjacency Matrix​

This is a 2D array where the rows represent source vertices and the columns represent destination vertices. Data at matrix[i][j] represents the edge weight between vertex i and vertex j. For unweighted graphs, this may simply be a binary value (0 or 1) indicating the presence or absence of an edge

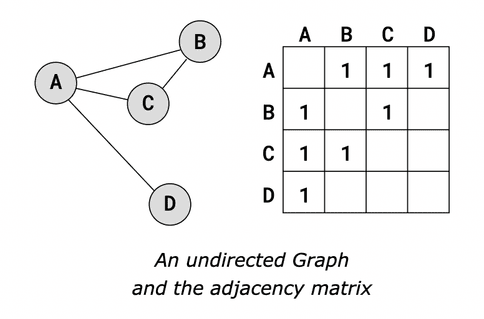
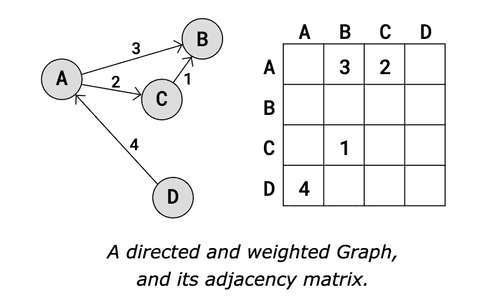
Adjacency Matrix Adjacency Matrix

Adjacency Matrix - representation

adjacency_matrix = [
    [0, 1, 1, 1],  # Edges for A
    [1, 0, 1, 0],  # Edges for B
    [1, 1, 0, 0],  # Edges for C
    [1, 0, 0, 0]   # Edges for D
]

Asymptotic Complexity 🕒 Time Complexity: The time complexity of BFS is O(V+E), where V is the number of vertices and E is the number of edges in the graph. This arises because each vertex and each edge will be explored in the worst case.

🌌 Space Complexity: The space complexity of BFS is O(V) as in the worst case, all vertices could be in the queue at the same time when the graph is like a complete graph.

Adjacency List​

This is a list where each element is a pair consisting of a vertex and a list of all the vertices that are connected to it by edges. This representation is more space-efficient for sparse graphs (graphs where the number of edges is much less than the number of vertices squared)

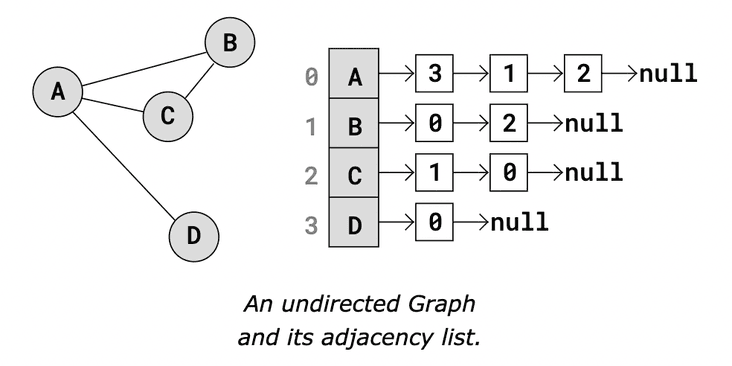
Adjacency List Adjacency List

Adjacency List - representation

const adjacency_list ={
	0: [1, 4]
	1: [0, 3, 4]
	2: [3]
	3: [1, 2, 4]
	4: [0, 1, 3]
}

Asymptotic Complexity
🕒 Time Complexity: The time complexity of DFS is O(V+E), where V is the number of vertices and E is the number of edges in the graph. This is because every vertex and every edge will be explored in the worst case

🌌 Space Complexity: The space complexity can be O(V) in the worst case due to the stack used for storing the vertices during the recursive traversal (or explicit stack in iterative versions).